This is a test case for the accuracy and sufficiency of the turbulence closure schemes implemented in the code.
Presently implemented is 2nd order Mellor Yamada (1982) in the vertical and Smagorinski (1963) in the horizontal.
Test Reference
- Rajaratnam, Nallamuthu and Nwachukwu, Benjamin A. (1983). "Flow Near Groin-Like Structures". Jounal of Hydraulic Engineering. Vol. 109, Issue 3 (January 1983).
Domain
- Flat, rectangular flume of 37.0 m length and 0.92 m width
- Emergent spur of length 0.152 m and width 0.03 m
- Spur placed 14.0 m downstream of the inflow location (at the left boundary)

Initial Conditions
- Smagorinski coefficient = 0.2
- Background kinematic eddy viscosity = 0.0015 m2/sec
- Manning's n = 0.01
Boundary Conditions
- Uniform flow of 0.0453 m3/sec
- Tailwater of 0.189 m
- No time varying boundary conditions
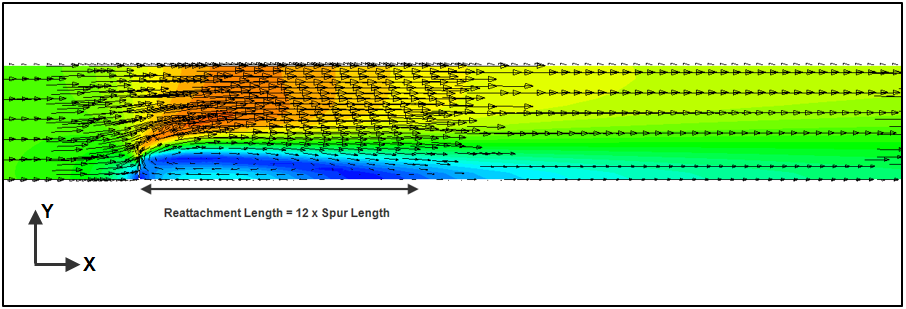
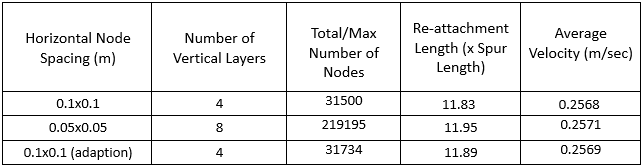
Results
- Model Computed Recirculation Zone at Steady State = 11.8 x Spur Length
- Wang et al. 2009 reports 12 times the spur length
References:
Mellor, G. L and Yamada, Tetsuji (1982). “Development of a Turbulence Closure Model for Geophysical Fluid Problems”, Reviews of Geophysics and Space Science, Vol. 20, No. 4, pp 851-875.
Smagorinsky, J. (1963). “General Circulation experiments with the primitive equations I. The basic experiment”. Monthly Weather Review, vol 91, No. 3, pp 99-164.
Wang, S. S. Y, Jia, Y, Roche, P.J, Smith, P.E and Schmalz, R.A (2009). “Verification and Validation of 3D Free Surface Flow Models”, American Society of Civil Engineering.